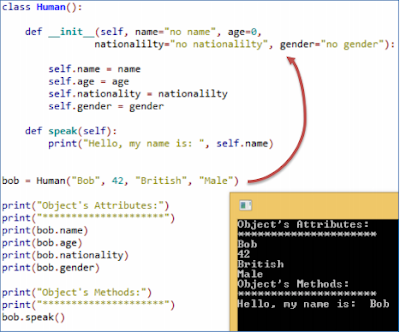
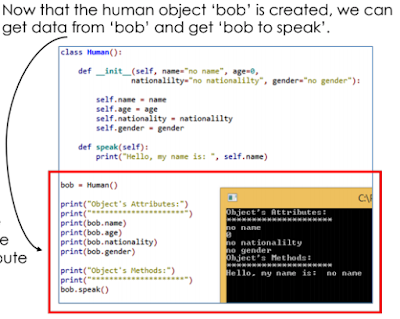
Simplifying Boolean Algebra
De Morgan's Law "Either logical function AND or OR may be replaced by each other, given certain changes to the equation." NOT (A OR B) = (NOT A) AND (NOT V) Distribution "Multiplying or factoring of an expression" A AND (B OR C) = (A AND B) OR (A AND C) Association "Allows for removal of brackets from an expression and regrouping of variables" A OR (B OR C) = (A OR B) OR C = A OR B OR C Commutation "The order of application of two separate values does not matter" A AND B = B AND A Double Negation "If you reverse something twice, you end up back where you started" THE NOT NOT OF A = A. Absorption "The second term inside the bracket can always be eliminated and 'absorbed' by the term outside the bracket if the given conditions are met" "Rules: Operators outside and inside bracket must be different. The term outside bracket must also be inside the bracket." X OR...